C2. Normal and Cooperative Binding of Dioxygen
- Page ID
- 4915
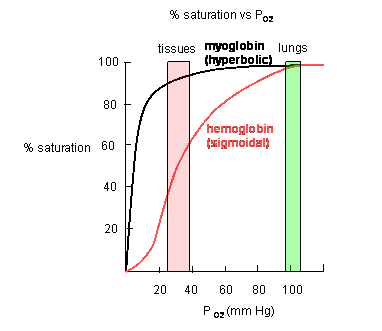
Plots of Y (fractional saturation) vs L (pO2) are hyperbolic for Mb, but sigmoidal for Hb, suggesting cooperative binding of oxygen to Hb (binding of the first oxygen facilitates binding of second, etc).
Figure: Plots of Y (fractional saturation) vs L (pO2) are hyperbolic for Mb, but sigmoidal for Hb
In another difference, the affinity of Hb, but not of Mb, for dioxygen depends on pH. This is called the Bohr effect, after the father of Neils Bohr, who discovered it.
Figure: Bohr effect
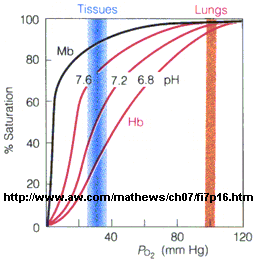
Protons (decreasing pH), carbon dioxide, and bisphosphoglycerate, all allosteric ligands which bind distal to the oxygen binding sites on the heme, shift the binding curves of Hb for oxygen to the right, lowering the apparent affinity of Hb for oxygen. The same effects do not occur for Mb. These ligands regulate the binding of dioxygen to Hb.
From these clues we wish to understand the molecular and mathematical bases for the sigmoidal binding curves, and binding that can be so exquisitely regulated by allosteric ligands. The two obvious features that differ between Mb and Hb are the tetrameric nature of Hb and its multiple (4) binding sites for oxygen. Regulation of dioxygen binding is associated with conformational changes in Hb.
Based on crystallographic structures, two main conformational states appear to exists for Hb, the deoxy (or T - taut) state, and the oxy (or R -relaxed) state. The major shift in conformation occurs at the alpha-beta interface, where contacts with helices C and G and the FG corner are shifted on oxygenation.
Figure: Conformation Changes on Oxygen Binding to Deoxy-Hemoglobin (files aligned with DeepView, displayed with Pymol)
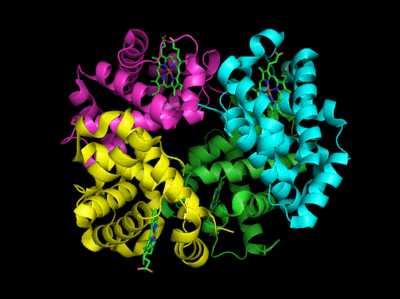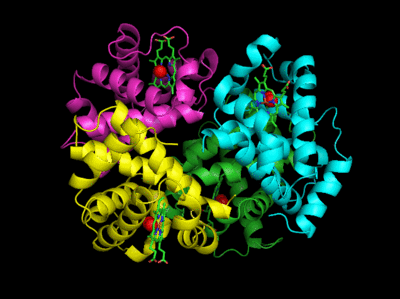
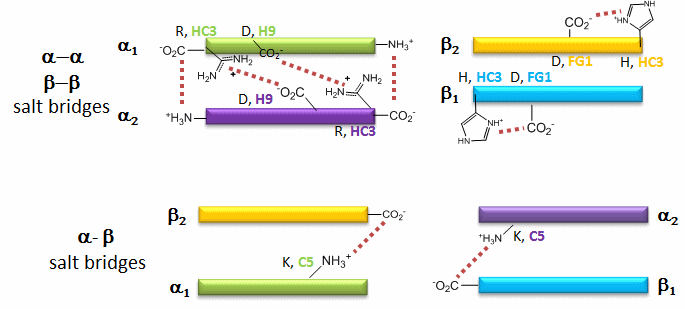
The deoxy or T form is stablized by 8 salt bridges which are broken in the transition to the oxy or R state.
Figure: Salt Bridges in Deoxy Hb
![]() Flash Movie: Salt Bridges in DeoxyHb
Flash Movie: Salt Bridges in DeoxyHb
6 of the salt bridges are between different subunits (as expected from the above analysis), with 4 of those involving the C- or N- terminus.
In addition, crucial H-bonds between Tyr 140 (alpha chain) or 145 (on the beta chain) and the carbonyl O of Val 93 (alpha chain) or 98 (beta chain) are broken. Crystal structures of oxy and deoxy Hb show that the major conformational shift occurs at the interface between the α and βsubunits. When the heme Fe binds oxygen it is pulled into the plan of the heme ring, a shift of about 0.2 nm. This small shift leads to larger conformational changes since the subunits are packed so tightly that compensatory changes in their arrangement must occur. The proximal His (coordinated to the Fe) is pulled toward the heme, which causes the F helix to shift, causing a change in the FG corner (the sequence separating the F and G helices) at the alpha-beta interface as well as the C and G helices at the interface, which all slide past each other to the oxy-or R conformation.
Decreasing pH shifts the oxygen binding curves to the right (to decreased oxygen affinity). Increased [proton] will cause protonation of basic side chains. In the pH range for the Bohr effect, the mostly likely side chain to get protonated is His (pKa around 6), which then becomes charged. The mostly likely candidate for protonation is His 146 (on the βchain - HC3) which can then form a salt bridge with Asp 94 of the β(FG1) chain. This salt bridge stabilizes the positive charge on the His and raises its pKa compared to the oxyHb state. Carbon dioxide binds covalently to the N terminus to form a negatively charge carbamate which forms a salt bridge with Arg 141 on the alpha chain. BPG, a strongly negatively charged ligand, binds in a pocket lined with Lys 82, His 2, and His 143 (all on the beta chain). It fits into a cavity present between the β subunits of the Hb tetramer in the T state. Notice all these allosteric effectors lead to the formation of more salt bridges which stabilize the T or deoxy state. The central cavity where BPG binds between the β subunits become much smaller on oxygen binding and the shift to the oxy or R state. Hence BPG is extruded from the cavity.
The binding of H+ and CO2 helps shift the equilibrium to deoxyHb which faciliates dumping of oxygen to the tissue. It is in respiring tissues that CO2 and H+ levels are high. CO2 is produced from the oxidation of glucose through glycolysis and the Krebs cycle. In addition, high levels of CO2 increase H+ levels through the following equilibrium:
\[\mathrm{H_2O + CO_2 \rightleftharpoons H_2CO_3 \rightleftharpoons H^+ + \sideset{}{_{3}^{-}}{HCO}}\]
In addition, H+ increases due to production of weak acids such as pyruvic acid in glycolysis .
Hb, by binding CO2 and H+, in addition to O2, serves an additional function: it removes excess CO2 and H+ from the tissues where they build up. When deoxyHb with bound H+ and CO2 reaches the lungs, they leave as O2 builds and deoxyHb is converted to oxyHb.


